God and Nature Winter 2023
Overcoming Paradox: a Lesson from Mathematics (2/3)
By Doug Phillippy
The infinite is an integral part of both mathematics and Christianity. Both rely heavily on its inclusion. Any attempt at explaining reality, whether in the abstract world of mathematics or the faith-based world of theology, will be incomplete or in error if the infinite is excluded from that explanation. When the human perception of reality is limited to a temporary existence in a natural world, the resulting worldview will be flawed. An inaccurate worldview can in turn manifest itself in paradox; that is, as something that seems contradictory or opposed to common sense with regard to that worldview, and yet may be true when understood from a proper worldview.
Jesus often made paradoxical statements to challenge the temporal worldview of his disciples. Unfortunately for Jesus’s disciples, and the rest of humanity, for that matter, life is experienced in the context of a physical birth and death, making it difficult for us to envision life beyond the confines of the womb and grave. In contrast, within the abstract world of mathematics, the infinite can be studied and manipulated, potentially overcoming paradox. In this essay I suggest that engaging in a mathematical exercise can reinforce the importance of including the eternal in our thinking if we wish to better understand some of Jesus’s seemingly paradoxical statements.
The infinite is an integral part of both mathematics and Christianity. Both rely heavily on its inclusion. Any attempt at explaining reality, whether in the abstract world of mathematics or the faith-based world of theology, will be incomplete or in error if the infinite is excluded from that explanation. When the human perception of reality is limited to a temporary existence in a natural world, the resulting worldview will be flawed. An inaccurate worldview can in turn manifest itself in paradox; that is, as something that seems contradictory or opposed to common sense with regard to that worldview, and yet may be true when understood from a proper worldview.
Jesus often made paradoxical statements to challenge the temporal worldview of his disciples. Unfortunately for Jesus’s disciples, and the rest of humanity, for that matter, life is experienced in the context of a physical birth and death, making it difficult for us to envision life beyond the confines of the womb and grave. In contrast, within the abstract world of mathematics, the infinite can be studied and manipulated, potentially overcoming paradox. In this essay I suggest that engaging in a mathematical exercise can reinforce the importance of including the eternal in our thinking if we wish to better understand some of Jesus’s seemingly paradoxical statements.
Thus a proper use of the infinite in the reasoning process eliminates paradox and contributes to a better understanding of reality. |
Mathematicians have often used the notion of paradox to identify weaknesses in the axiomatic systems they use. The barber paradox was posed in 1918 by Bertrand Russell (who attributed it to an unnamed source) to illustrate the problems with unrestricted use of the mathematical concept of set. In short, this paradox asks: if a barber in a certain town cuts the hair of all those, and only those, who never cut their own hair, does the barber cut his own hair? Long before Russell, Zeno (circa 450 B.C.) posed several problems to illustrate problems with the Greek understanding of the concepts of line and point. The Greeks believed that time and space could be broken up into tiny units called points and instants. Zeno’s puzzles proved problematic within that framework, and therefore have become known as Zeno’s paradoxes even though they may not seem very paradoxical to the modern mathematician.
These paradoxes include Dichotomy, Achilles, Arrow, and the Stade. The most famous of these is probably that of Achilles. In this story, a tortoise challenges the speedy Achilles to a race. It is known that Achilles is ten times as fast as this particular tortoise. The tortoise insists that if given a 100-meter head start, Achilles will never catch him. The tortoise’s explanation for this claim seems reasonable. He describes an infinite sequence of instants during which Achilles remains behind the tortoise. Using the Greek understanding of space and time, the tortoise concludes that he always remains ahead of the speedy Achilles. The tortoise reasons that after Achilles has traveled 100 meters, thus making up the initial head start, he (the tortoise) will have traveled 10 meters and still maintain the lead. While Achilles travels those 10 meters, the tortoise travels one more meter, and after Achilles traverses that meter, the tortoise will still have a tenth of a meter lead. Thus the tortoise describes an infinite process during which he always remains ahead of Achilles. Although his lead is shrinking, the tortoise will in fact remain ahead of Achilles at any step of this process. However, this particular explanation is based on the misconception that an infinite process cannot yield a finite result.
This paradox is easily explained by what mathematicians know as a geometric series. A geometric series is an infinite summation of the form:
a + ar + ar^2 + ar^3 + .... It is known that this series converges if | r | < 1 and the sum is a/(1 - r). For example, if a = 1 and r =½, the infinite series becomes
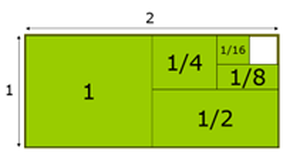
1 + ½ + ¼ + 1/8 + … = 1/(1 – ½) = 2. This result is easily visualized by taking a rectangle of length 2 and width 1 and repeatedly cutting it in half (see the diagram, where the numbers represent the area of the respective rectangle that they are in).
The Greek understanding of the very small is the source of the paradox in the story of Achilles and the tortoise. By allowing time and space to be viewed as a continuum with infinitesimally small components and not as a sequence of distinct instants and points, the result of the race is anything but paradoxical. Using the geometric series with a = 100, and r = 1/10, it is easily seen that Achilles is the winner of any race that is longer than 111.111... meters. The tortoise can only win a race that is shorter than this length. Thus a proper use of the infinite in the reasoning process eliminates paradox and contributes to a better understanding of reality.
Similar reasoning is required to properly understand many of the paradoxical statements found in Scripture. For example, consider this particular statement of Jesus: “So the last will be first, and the first will be last.” As Matthew turns his attention toward the conclusion of his telling of the gospel story, his focus shifts to Jesus’s coming kingdom, and he records a series of questions posed to Jesus by various people interested in that kingdom (Matthew 18-20). The gospel-writer highlights some of Jesus’s parables about salvation and forgiveness, as well as his interactions with children and some of his questioners, including a rich young ruler. As he tells this portion of the gospel story, Matthew refers to this statement of Jesus several times (see Matthew 19:30; 20:16, 26-27).
Taken from a temporal perspective, these words of Jesus are difficult to understand. One possible interpretation from this perspective is that life is essentially a “dead heat”—that is, everyone finishes in a tie. While some truth may be gleaned from this interpretation, the context suggests something more is intended. Jesus used these very words to conclude a parable he told about workmen who were hired at different times throughout the workday and yet received the same wages. In this parable, those who were hired first were actually paid last and witnessed the later hires receiving the same pay they too would receive. As a result, those who worked the entire day grumbled against the landowner who hired them. From their perspective, they had been treated unfairly. In a similar way, if we understand Jesus’s words only in the context of our existence here on earth, they seem paradoxical, undoubtedly leading us to the same conclusion as the Psalmist, who, after observing the prosperity of the wicked, said, “Surely in vain have I kept my heart pure; in vain have I washed my hands in innocence” (Psalm 73:13).
To properly understand Jesus’s words, we must understand the context in which they were spoken. The parable is about the kingdom of heaven, and as was noted previously, is recorded by Matthew in the midst of several teachings about who is the greatest in the kingdom of heaven (see Matthew 18:1-9; Matthew 20:20-28). It immediately follows Jesus’s challenge to a rich young ruler to sell what he owned, give it to the poor, and follow Jesus in order to obtain eternal life. The context here (eternal) suggests something more than a temporal, earthly understanding of reality. Unfortunately, the young ruler did not have this perspective and walked away disheartened by Jesus’s challenge.
The young ruler serves as an example of how difficult it is to have an eternal perspective. Like the Psalmist mentioned above, who said, “When I tried to understand all this, it was oppressive to me till I entered the sanctuary of God; then I understood their final destiny” (Psalm 73:16, 17), it is all too easy to have the wrong perspective regarding our place (and the place of others) in life. Earthly riches, success, and power (or lack thereof) often form the basis for determining who is first and last in life, making Jesus’s declaration concerning the first and last seem paradoxical. But the words of Jesus are paradoxical precisely because they are understood from within a temporal context. Because this temporal context is our natural context, Zeno’s paradox of Achilles can serve as a great reminder of how removing the infinite from our reasoning creates paradox, and how, in turn, the inclusion of the infinite can help to overcome that paradox. My hope is that this essay encourages us to step into the sanctuary of God where we can view life from a different vantage point, one that expands our view of reality beyond our earthly existence and allows us to say with the Psalmist, “Whom have I in heaven but you? And earth has nothing I desire besides you” (Psalm 73:25).
Dr. Phillippy is a Professor of Mathematics at Messiah University located in Grantham, Pennsylvania. He received his Ph.D. (1991) from Lehigh University, where he was trained as an applied mathematician. Since coming to Messiah College, his research interests have shifted to include the integration of faith and mathematics and developing mathematical maturity at the undergraduate level. On a personal note, Dr. Phillippy is a runner and enjoys participating in a variety of other sports. He is married to Deb and has four children.
These paradoxes include Dichotomy, Achilles, Arrow, and the Stade. The most famous of these is probably that of Achilles. In this story, a tortoise challenges the speedy Achilles to a race. It is known that Achilles is ten times as fast as this particular tortoise. The tortoise insists that if given a 100-meter head start, Achilles will never catch him. The tortoise’s explanation for this claim seems reasonable. He describes an infinite sequence of instants during which Achilles remains behind the tortoise. Using the Greek understanding of space and time, the tortoise concludes that he always remains ahead of the speedy Achilles. The tortoise reasons that after Achilles has traveled 100 meters, thus making up the initial head start, he (the tortoise) will have traveled 10 meters and still maintain the lead. While Achilles travels those 10 meters, the tortoise travels one more meter, and after Achilles traverses that meter, the tortoise will still have a tenth of a meter lead. Thus the tortoise describes an infinite process during which he always remains ahead of Achilles. Although his lead is shrinking, the tortoise will in fact remain ahead of Achilles at any step of this process. However, this particular explanation is based on the misconception that an infinite process cannot yield a finite result.
This paradox is easily explained by what mathematicians know as a geometric series. A geometric series is an infinite summation of the form:
a + ar + ar^2 + ar^3 + .... It is known that this series converges if | r | < 1 and the sum is a/(1 - r). For example, if a = 1 and r =½, the infinite series becomes
1 + ½ + ¼ + 1/8 + … = 1/(1 – ½) = 2. This result is easily visualized by taking a rectangle of length 2 and width 1 and repeatedly cutting it in half (see the diagram, where the numbers represent the area of the respective rectangle that they are in).
The Greek understanding of the very small is the source of the paradox in the story of Achilles and the tortoise. By allowing time and space to be viewed as a continuum with infinitesimally small components and not as a sequence of distinct instants and points, the result of the race is anything but paradoxical. Using the geometric series with a = 100, and r = 1/10, it is easily seen that Achilles is the winner of any race that is longer than 111.111... meters. The tortoise can only win a race that is shorter than this length. Thus a proper use of the infinite in the reasoning process eliminates paradox and contributes to a better understanding of reality.
Similar reasoning is required to properly understand many of the paradoxical statements found in Scripture. For example, consider this particular statement of Jesus: “So the last will be first, and the first will be last.” As Matthew turns his attention toward the conclusion of his telling of the gospel story, his focus shifts to Jesus’s coming kingdom, and he records a series of questions posed to Jesus by various people interested in that kingdom (Matthew 18-20). The gospel-writer highlights some of Jesus’s parables about salvation and forgiveness, as well as his interactions with children and some of his questioners, including a rich young ruler. As he tells this portion of the gospel story, Matthew refers to this statement of Jesus several times (see Matthew 19:30; 20:16, 26-27).
Taken from a temporal perspective, these words of Jesus are difficult to understand. One possible interpretation from this perspective is that life is essentially a “dead heat”—that is, everyone finishes in a tie. While some truth may be gleaned from this interpretation, the context suggests something more is intended. Jesus used these very words to conclude a parable he told about workmen who were hired at different times throughout the workday and yet received the same wages. In this parable, those who were hired first were actually paid last and witnessed the later hires receiving the same pay they too would receive. As a result, those who worked the entire day grumbled against the landowner who hired them. From their perspective, they had been treated unfairly. In a similar way, if we understand Jesus’s words only in the context of our existence here on earth, they seem paradoxical, undoubtedly leading us to the same conclusion as the Psalmist, who, after observing the prosperity of the wicked, said, “Surely in vain have I kept my heart pure; in vain have I washed my hands in innocence” (Psalm 73:13).
To properly understand Jesus’s words, we must understand the context in which they were spoken. The parable is about the kingdom of heaven, and as was noted previously, is recorded by Matthew in the midst of several teachings about who is the greatest in the kingdom of heaven (see Matthew 18:1-9; Matthew 20:20-28). It immediately follows Jesus’s challenge to a rich young ruler to sell what he owned, give it to the poor, and follow Jesus in order to obtain eternal life. The context here (eternal) suggests something more than a temporal, earthly understanding of reality. Unfortunately, the young ruler did not have this perspective and walked away disheartened by Jesus’s challenge.
The young ruler serves as an example of how difficult it is to have an eternal perspective. Like the Psalmist mentioned above, who said, “When I tried to understand all this, it was oppressive to me till I entered the sanctuary of God; then I understood their final destiny” (Psalm 73:16, 17), it is all too easy to have the wrong perspective regarding our place (and the place of others) in life. Earthly riches, success, and power (or lack thereof) often form the basis for determining who is first and last in life, making Jesus’s declaration concerning the first and last seem paradoxical. But the words of Jesus are paradoxical precisely because they are understood from within a temporal context. Because this temporal context is our natural context, Zeno’s paradox of Achilles can serve as a great reminder of how removing the infinite from our reasoning creates paradox, and how, in turn, the inclusion of the infinite can help to overcome that paradox. My hope is that this essay encourages us to step into the sanctuary of God where we can view life from a different vantage point, one that expands our view of reality beyond our earthly existence and allows us to say with the Psalmist, “Whom have I in heaven but you? And earth has nothing I desire besides you” (Psalm 73:25).
Dr. Phillippy is a Professor of Mathematics at Messiah University located in Grantham, Pennsylvania. He received his Ph.D. (1991) from Lehigh University, where he was trained as an applied mathematician. Since coming to Messiah College, his research interests have shifted to include the integration of faith and mathematics and developing mathematical maturity at the undergraduate level. On a personal note, Dr. Phillippy is a runner and enjoys participating in a variety of other sports. He is married to Deb and has four children.
