God and Nature Spring 2023
In Pursuit of the Infinite: Living in Paradox 3/3
By Doug Phillippy
But Christ has indeed been raised from the dead, the first fruits of those who have fallen asleep.
(1 Corinthians 15:20)
When fallen human beings seek to understand an infinite God, they often impose their imperfect understanding of reality on him. In the process, God can be trivialized, made to look more like his creation than the infinite being he is. The Old Testament character Job was guilty of this. As he interacted with his friends, trying to make sense of why God would allow him to experience all the calamity that had come upon him, he said, “If only I knew where to find him; if only I could go to his dwelling! I would state my case before him and fill my mouth with arguments. I would find out what he would answer me, and consider what he would say” (Job 23:3-5).
When Job finally gets his chance to stand before God, it is not Job, but God who does the questioning. “Where were you when I laid the earth's foundation? Tell me, if you understand” (Job 38:4). God then proceeds to fire question after question at Job, asking for a response. Job can only respond by saying, "I am unworthy—how can I reply to you? I put my hand over my mouth. I spoke once, but I have no answer—twice, but I will say no more" (Job 40:4-5). Job explains his change of heart, stating, “Surely I spoke of things I did not understand, things too wonderful for me to know” (Job 42:3), adding, “My ears had heard of you but now my eyes have seen you. Therefore I despise myself and repent in dust and ashes" (Job 42:5-6). Coming face-to-face with the infinite God changed Job’s perspective of both God and himself.
We won’t all get a face-to-face intervention from God to correct our short-sighted estimation of who he is in the way Job did. However, we can encounter the infinite readily in our study of mathematics. This is the third in a series of essays that examines the question of whether or not “seeing” the infinite on display in mathematics can impact our understanding of an infinite God. In the second essay, “Overcoming Paradox: A Lesson from Mathematics” (Winter 2023), we considered the equation: 1/2 + 1/4 + 1/8 + 1/16 + … = 1,
which all mathematicians would hold as true, recognizing the left-hand side of this equation as a geometric series.
I then offered the geometric series as a response to Zeno’s paradox of the tortoise and Achilles, and used it as an example of how a proper consideration of the infinite in the reasoning process can eliminate paradox and contribute to a better understanding of reality. In this essay, I would like to continue the discussion, this time exploring the potential for the inclusion of the infinite to actually create paradox in our understanding of reality. Davis and Hersh hint at this, stating the following regarding the above statement of equality: “On the left-hand side we seem to have incompleteness, infinite striving. On the right-hand side we have finitude, completion. There is a tension between the two sides which is a source of power and paradox” (1).
The very nature of calculus forces those who study it to expand their understanding of mathematics. But this stretching of the mind is not limited to new concepts (like the limit) encountered in class; it includes rethinking some of the most fundamental properties of the discipline. One such property is the commutative property of addition, which states that the order in which numbers are summed does not matter, and is drilled into the heads of students beginning in elementary school. By the time they are introduced to infinite series in a Calculus class, the commutative property of addition is a forgone conclusion.
In a typical Calculus course students encounter the alternating harmonic series:
But Christ has indeed been raised from the dead, the first fruits of those who have fallen asleep.
(1 Corinthians 15:20)
When fallen human beings seek to understand an infinite God, they often impose their imperfect understanding of reality on him. In the process, God can be trivialized, made to look more like his creation than the infinite being he is. The Old Testament character Job was guilty of this. As he interacted with his friends, trying to make sense of why God would allow him to experience all the calamity that had come upon him, he said, “If only I knew where to find him; if only I could go to his dwelling! I would state my case before him and fill my mouth with arguments. I would find out what he would answer me, and consider what he would say” (Job 23:3-5).
When Job finally gets his chance to stand before God, it is not Job, but God who does the questioning. “Where were you when I laid the earth's foundation? Tell me, if you understand” (Job 38:4). God then proceeds to fire question after question at Job, asking for a response. Job can only respond by saying, "I am unworthy—how can I reply to you? I put my hand over my mouth. I spoke once, but I have no answer—twice, but I will say no more" (Job 40:4-5). Job explains his change of heart, stating, “Surely I spoke of things I did not understand, things too wonderful for me to know” (Job 42:3), adding, “My ears had heard of you but now my eyes have seen you. Therefore I despise myself and repent in dust and ashes" (Job 42:5-6). Coming face-to-face with the infinite God changed Job’s perspective of both God and himself.
We won’t all get a face-to-face intervention from God to correct our short-sighted estimation of who he is in the way Job did. However, we can encounter the infinite readily in our study of mathematics. This is the third in a series of essays that examines the question of whether or not “seeing” the infinite on display in mathematics can impact our understanding of an infinite God. In the second essay, “Overcoming Paradox: A Lesson from Mathematics” (Winter 2023), we considered the equation: 1/2 + 1/4 + 1/8 + 1/16 + … = 1,
which all mathematicians would hold as true, recognizing the left-hand side of this equation as a geometric series.
I then offered the geometric series as a response to Zeno’s paradox of the tortoise and Achilles, and used it as an example of how a proper consideration of the infinite in the reasoning process can eliminate paradox and contribute to a better understanding of reality. In this essay, I would like to continue the discussion, this time exploring the potential for the inclusion of the infinite to actually create paradox in our understanding of reality. Davis and Hersh hint at this, stating the following regarding the above statement of equality: “On the left-hand side we seem to have incompleteness, infinite striving. On the right-hand side we have finitude, completion. There is a tension between the two sides which is a source of power and paradox” (1).
The very nature of calculus forces those who study it to expand their understanding of mathematics. But this stretching of the mind is not limited to new concepts (like the limit) encountered in class; it includes rethinking some of the most fundamental properties of the discipline. One such property is the commutative property of addition, which states that the order in which numbers are summed does not matter, and is drilled into the heads of students beginning in elementary school. By the time they are introduced to infinite series in a Calculus class, the commutative property of addition is a forgone conclusion.
In a typical Calculus course students encounter the alternating harmonic series:
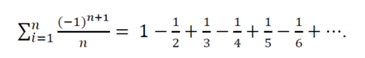
It is easy to show that the sum of this infinite series must be between ½ and 1. By arranging the terms in pairs: (1 - 1/2) + (1/3 - 1/4) + (1/5 - 1/6) + …, it is easy to verify that the sum is at least ½ because the sum of the first pair is ½, and the sum of each successive pair is greater than 0. Partial sums consisting of the first, second, and third pairs (to three decimal places) are: .5, .583, and .617, respectively. A slightly different arrangement of the same terms, 1 – (1/2 - 1/3) – (1/4 - 1/5) – (1/6 – 1/7) - …, shows that the sum must be less than 1 because the sum of each pair in parentheses is greater than 0, and each pair is subtracted from 1. In other words, when the summands are arranged in pairs, it is clear that the sum lies somewhere between ½ and 1.
However, a third arrangement of the terms (in triplets) is (1 + 1/3 - 1/2) + (1/5 + 1/7 - 1/4) + (1/9 + 1/11 - 1/6) + …. It is easy to show that each triplet in the infinite sum is greater than zero so that as successive triplets are added, the corresponding sequence of partial sums will increase. Moreover, the partial sum of the first seven triplets is 1.005 (to 3 decimal places). Thus, when the positive terms in this summation are summed twice as fast as the negative terms, the exact same summands yield a completely different sum. The first 50 partial sums for the two different arrangements are plotted in the graph below (the pairs in red, the triplets in blue), showing that the two different arrangements of terms converge to two different sums.
It is easy to show that the sum of this infinite series must be between ½ and 1. By arranging the terms in pairs: (1 - 1/2) + (1/3 - 1/4) + (1/5 - 1/6) + …, it is easy to verify that the sum is at least ½ because the sum of the first pair is ½, and the sum of each successive pair is greater than 0. Partial sums consisting of the first, second, and third pairs (to three decimal places) are: .5, .583, and .617, respectively. A slightly different arrangement of the same terms, 1 – (1/2 - 1/3) – (1/4 - 1/5) – (1/6 – 1/7) - …, shows that the sum must be less than 1 because the sum of each pair in parentheses is greater than 0, and each pair is subtracted from 1. In other words, when the summands are arranged in pairs, it is clear that the sum lies somewhere between ½ and 1.
However, a third arrangement of the terms (in triplets) is (1 + 1/3 - 1/2) + (1/5 + 1/7 - 1/4) + (1/9 + 1/11 - 1/6) + …. It is easy to show that each triplet in the infinite sum is greater than zero so that as successive triplets are added, the corresponding sequence of partial sums will increase. Moreover, the partial sum of the first seven triplets is 1.005 (to 3 decimal places). Thus, when the positive terms in this summation are summed twice as fast as the negative terms, the exact same summands yield a completely different sum. The first 50 partial sums for the two different arrangements are plotted in the graph below (the pairs in red, the triplets in blue), showing that the two different arrangements of terms converge to two different sums.
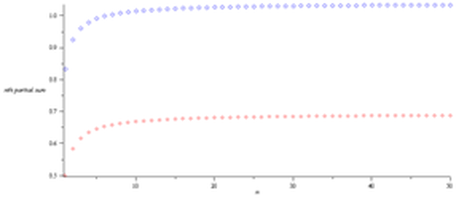
This surprising outcome is a direct consequence of summing an infinite number of terms and is contrary to what is experienced when adding a finite number of terms. It is important to note that mathematicians have done a lot of work to shore up the theory associated with infinite series, including development of the concept of absolute convergence, which precludes the possibility of two different arrangements of the same series resulting in different sums.
However, this was not the case yet in 1807 when Joseph Fourier proposed a solution to a heat conduction problem that included an infinite series. Contemporaries of Fourier could have rejected his work outright because it made use of ideas that challenged their understanding. Or, they could have blindly extended the rules that they knew were true in the realm of the finite to the infinite. Instead, many of Fourier’s peers sought to establish appropriate restrictions under which those rules could be applied. As a result of their investigation, they gained a much deeper understanding of infinite summation. Regarding this time period in the history of mathematics, David Bressoud said, “The nineteenth century would see ever expanding investigations into the assumptions of calculus, an inspection and refitting of the structure from the footings to the pinnacle, so thorough a reconstruction that calculus was given a new name: Analysis. Few…would have recognized mathematics as it stood one hundred years later” (2).
I offer the above discussion regarding the development of infinite series in mathematics as a model of what can happen when finite human beings seek to understand an infinite God. In particular, I make two observations. First, just as working with the infinite in mathematics can yield unexpected results, pursuit of an infinite God can challenge established assumptions about reality, perhaps even creating paradox in the mind of the one in pursuit (at least temporarily).
Second, challenged assumptions and an incomplete understanding of reality should not be used as an excuse to remain in paradox, but instead should be seen as an opportunity to reshape how reality is perceived. In the same way that mathematics, and ultimately those who practice the discipline, are stretched by incorporating the infinite into the reasoning process, so it should be for those who seek to know our infinite God.
Perhaps there is no time more relevant than Easter to apply these observations. The first Easter introduced humanity to the reality of the empty tomb, and today those who contemplate this possibility are forced to rethink what they thought they knew about life and death. In fact, Jesus’s resurrection compels his followers to re-envision life here on this earth as something more than a temporary existence that is shrouded in the sting of death, and consider it in light of the hope of their own resurrection as well. This new take on reality, together with Jesus’s teaching that those who follow him must deny themselves and daily take up their own cross (Matthew 16:24,25), is certain to create paradox within those who wish to fully follow him. But those who take this challenge and live within that paradox can take heart because they have the promise of Jesus that it is in the process of losing their life that they can truly find it.
References
- Davis, Phillip and R. Hersh, The Mathematical Experience. Boston: Houghton-Mifflin, 1999.
- Bressoud, David, A Radical Approach to Real Analysis. The Mathematical Association of America, 1994.
Dr. Phillippy is a Professor of Mathematics at Messiah University located in Grantham, Pennsylvania. He received his Ph.D. (1991) from Lehigh University, where he was trained as an applied mathematician. Since coming to Messiah College, his research interests have shifted to include the integration of faith and mathematics and developing mathematical maturity at the undergraduate level. On a personal note, Dr. Phillippy is a runner and enjoys participating in a variety of other sports. He is married to Deb and has four children.
